第六話「7つの橋を渡れ 」
「数学ができない日本人は、カレー屋になったほうが良い」と言われて、途方に暮れて、とぼとぼと、足取り重く本屋へ向かった。まさか、今から受験参考書というわけにも行かないので、自然科学の棚で数学の本を探した。代数学、幾何学、解析学あたりは名前を知っていたが、トポロジー(注1)というものがあるらしいことがわかった。
そこで、今日習っていたことに関連する本を見つけ、パラパラとめくっているとそこには、地図のようなものに「ケーニヒスベルクの7つの橋」問題と書いてあった。
18世紀初頭にオイラー(Euler)という天才数学者がいた。オイラーの時代、ロシアのケーニヒスベルグ(Konigsberg)という町を流れるプレーゲル川には、中央に島があって、その島と川の両岸との間には図1のように7つの橋がかかっていたという。昔から、その町に住む人々が議論していた問題は、「7つの橋すべてを、1つの橋を複数回渡ることなくすべて渡り終えるような橋の渡り方を見つけられるのか?」であった。
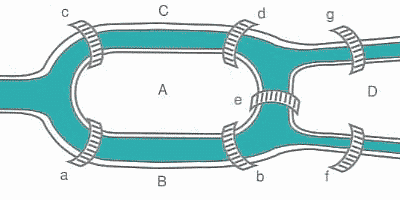 図1.
図1. 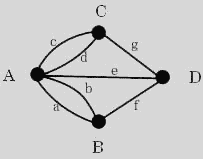 図2.
図2.
オイラーは「そのような渡り方は不可能」と、答えを導き出した。(後に「オイラーの一筆書きの定理」と呼ばれるようになった。)一体、オイラーは、どうやって、この問題を解いたのだろうか? ここで、グラフ理論が登場する。グラフ理論とは、簡単に言えば、幾つかの点と、それを結ぶ幾つかの辺からなる図形を『グラフ(graph)』と定義し、その構造の性質を研究する数学のことである。同じ数学といっても、学校で習っていた微分積分・代数学とはかなり様子が異なるが、どちらかといえば、論理学に近い感じである。オイラーは、その問題の解答に到達するために図2のように陸地を頂点(vertices)、橋を辺(edge)とするグラフで問題を表現し、証明したと言われている。
この「問題の構造を表現し理解するために」数学を使うという事実に、ショックを受けた。そんなふうに、数学を使うなんて、いままで知らなかった。それは、まるで日常生活の中で、何か相手に伝えようとして言葉で表現しているかのように必要があれば分かりやすく絵を書いて説明するかのように使われていた。ここでは、数学は言葉や絵と同様にコミュニケーションの道具の一つなのだった。
その後、グラフ理論は、数学でありながら、ネットワークや集積回路などのコンピュータに関係がある分野に数多く使用されていることもわかった。しかし、なにしろ数学だけに、理解さえできれば便利かもしれないが、「分かる人には分かるが、分からない人には、さっぱりわからん!」というのも、まぎれもない事実だ。「7つの橋は一筆書きで渡れない」ように、こちら(数学)も、どうやら一筋縄ではいかないようである。
(注1)トポロジー(topology)
任意の空間と、その空間内の要素の位置や場所に関して定義される論理のこと。
ここでいう論理には、各要素の上下関係、前後関係、集合論的関係、時間的順序などがある。
参考文献:Lafore,
Robert【著】・岩谷 宏【訳】「Javaで学ぶアルゴリズムとデータ構造」ソフトバンク (1999-01-14出版)
(2002年8月)
